U Image Processing toolboxu nalaze se funkcije specijalizovane za ulazno-izlazne operacije, prikazivanje i obradu slika. Da biste vidjeli listu svih funkcija u ovom toolboxu otkucajte help images u Matlab komandnoj liniji. Vidimo da je na raspolaganju veliki broj funkcija. Mi ćemo se u okviru laboratorijskih vježbi iz Digitalne obrade slike dotaći samo nekih.
Matlab memoriše sliku kao matricu. Svakom pikselu na slici odgovara jedan element matrice. Elementi matrice mogu biti klase double što znači da se svaki pamti kao 64-bitni broj u plivajućem zarezu. Međutim, na ovaj način slike mogu zauzimati izuzetno mnogo memorije. Npr. slika dimenzija 1000x1000 zahtijevala bi oko 8 megabajta prostora. Zbog toga je u Matlabu uvedena i klasa uint8 koja omogućava da se svaki element matrice (piksel) memoriše kao 8-bitni cijeli broj.
Podržana su četiri osnovna tipa slika koji se javljaju i u poznatim rasterskim grafičkim programima kao što su Adobe Photoshop i PaintShop Pro.
uint8. Da biste saznali ponešto o njihovim specifičnostima otkucajte help uint8.
Indeksirane slike se memorišu kao dvije matrice, matrica slike i kolormapa. Kolormapa sadrži vrijednosti koje predstavljaju boje piksela u slici. Matrica slike za svaki piksel sadrži indeks elementa u kolormapi koji predstavlja boju tog elementa.
Kolormapa je matrica klase double dimenzija m x 3. Svaka vrsta kolormape sadrži vrijednosti crvene (R), zelene (G) i plave (B) komponente određene boje. R, G i B su realni skalari čije su vrijednosti iz opsega od 0 (crna) do 1.0 (pun intenzitet).
Elementi matrice slike mogu biti klase double ili uint8. Ukoliko se radi o klasi uint8 onda reprezentacija slike odgovara standardnoj reprezentaciji 8-bitnih indeksiranih slika u grafičkim fajlovima.
Matlab čuva intenzitetsku sliku kao jednu matricu u kojoj svaki element odgovara jednom pikselu slike. Matrica može biti klase double u kom slučaju su njeni elementi iz opsega [0,1] ili klase uint8 sa elementima iz opsega [0,255]. Elementi matrice predstavljaju intenzitet (nivo sivila) pojedinih piksela, gdje vrijednost 0 odgovara crnoj, a 1 (odnosno 255) punom intenzitetu, tj. bijeloj boji.
U binarnoj slici svaki piksel može poprimiti jednu od dvije moguće vrijednosti. Ove vrijednosti mogu se tumačiti kao objekat i kao pozadina. Matlab binarnu sliku memoriše kao matricu čiji elementi su 0 (pozadina) i 1 (objekat). Jasno, binarna slika može se posmatrati kao specijalan slučaj intenzitetske slike sa samo dva nivoa intenziteta.
Elementi matrice mogu biti klase double ili klase uint8. Sa stanovišta utroška memorije daleko je povoljnije korišćenje klase uint8. Pomoću jedne logičke promjenljive Matlab vodi računa o tome da li se radi o binarnoj slici, tj. kako treba interpretirati elemente matrice.
Kao kod indeksiranih slika i kod RGB slika se boja piksela određuje na osnovu tri komponente R, G i B. Međutim, za razliku od indeksiranih slika kod koji se vrijednosti ovih komponenti čuvaju u posebnoj kolormapi, kod RGB slika one se pamte u samoj matrici slike.
Dakle, matrica slike je dimenzija m x n x 3, gdje sum i n broj vrsta, odnosno kolona matrice slike. Može se smatrati da se treća dimenzija sastoji od tri ravni čijom kombinacijom se dobijaju boje piksela.
Matlab omogućava konverzije između različitih tipova slika. Za više informacija pogledati funkcije iz sekcije Image types and type conversions u Image Processing Toolboxu.
U zavisnosti od situacije lokacije piksela na slici mogu se odrediti različitim koordinatnim sistemima. Image Processing Toolbox koristi dva koordinatna sistema:
U ovom koordinatnom sistemu slika se postmatra kao rešetka sa diskretnim elementima uređenim odozgo prema dole i sa lijeva u desno, kao na slici.
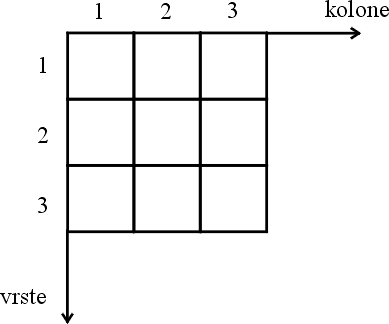
Očigledno, postoji jednoznačna korespondencija između ovako definisanih koordinata piksela i indeksa elemenata matrice u Matlabu.
U koordinatnom sistemu piksela pikseli se posmatraju kao diskretni elementi koji nemaju dimenzija. Pojedinim pikselima pristupa se navodjenjem njihovih koordinata koje su cjeli brojevi, npr. (2,3). Koordinate (2.3,3.4) nemaju smisla.
Ponekad je međutim pogodno piksel posmatrati kao kvadratnu oblast koja ima neku konačnu površinu. Sada pozicija (2.3,3.4) ima smisla i različita je od pozicije (2,3). Prostorni koordinatni sistem ilustrovan je sledećom slikom:
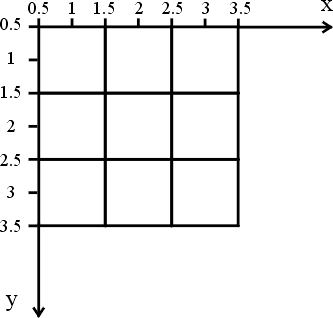
Vidimo da su koordinate centra svakog piksela u prostornom koordinatnom sistemu iste kao i koordinate tog piksela u koordinatnom sistemu piksela. Sa druge strane, razlikuju se ishodišta koordinatnih sistema, kao i redoslijed horizontalne i vertikalne koordinate.