Digitalni filtri

Predstavljanje digitalnih signala u MATLAB-u

Budući da je digitalni signal sekvenca (niz) brojeva njihovo predstavljanje u MATLAB-u je očigledno – pomoću MATLAB-ovih nizova (vektora) čiji su elementi odmjerci signala sa kojim radimo. Najvažnija razlika u odnosu na kontinualne signale je da je ovo potpuna reprezentacija signala, tj. mimo ovih odmjeraka signal nije definisan.

Za vizuelno predstavljanje digitalnih (diskretnih signala) povoljnija je komanda stem, čija je sintaksa ista kao i sintaksa ranije pomenute komande plot.

Centralnu ulogu u linearnoj obradi signala igra Furijeova transformacija, tj. u slučaju diskretnih signala diskretna Furijeova transformacija (DFT). U MATLAB-u je DFT implementirana kao brza Furijeova transformacija (FFT) i za njeno izračunavanje se koriste sledeće funkcije:

Zadaci

1. Generisati 128 odmjeraka svakog od signala 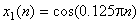 i .
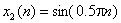   1. Nacrtati dobijene signale;
   2. Izračunati DFT ovih signala i nacrtati njen realni i imaginarni dio;
   3. Nacrtati magnitudu DFT signala.
   4. Uporedite spektre ova dva signala. Koje su njihove sličnosti i razlike. Da li spektri izgledaju onako kako ste očekivali?
   5. Rekonstruišite signale na osnovu njihovih spektara, tj. odredite inverznu Furijeovu transformaciju. Uvjerite se da se ponovo dobijaju polazni signali. Pri ovome imajte u vidu da Furijeova transformacija i inverzna Furijeova transformacija kao rezultat daju kompleksne veličine.
2. Generisati 128 odmjeraka signala .
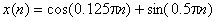   1. Nacrtati dobijene signale;
   2. Izračunati DFT ovih signala i nacrtati njen realni i imaginarni dio;
   3. Nacrtati magnitudu DFT signala.
   4. Rekonstruišite signale na osnovu njihovih spektara, tj. odredite inverznu Furijeovu transformaciju. Uvjerite se da se ponovo dobijaju polazni signali.

Analiza i simulacija digitalnih filtara

Jedan od načina zadavanja digitalnih filtara u MATLAB-u je pomoću njihove funkcije prenosa. Poznato je da funkcija prenosa ovakvih sistema ima oblik racionalne funkcije. Dakle, moguće je memorisati dva polinoma, b i a, koji predstavljaju brojnik i nazivnik funkcije prenosa.

Za analizu digitalnih filtara koriste se sledeće naredbe/funkcije.

Za određivanje frekvencijske karakteristike filtra koristi se funkcija freqz čija je sintaksa:

[h, f] = freqz(b, a, N, Fs);

gdje su b i a brojnik i nazivnik funkcije prenosa filtra, respektivno, N je broj tačaka u kojima se izračunava frekvencijska karakteristika, a Fs je frekvencija odmjeravanja. U vektoru h nalaze se vrijednosti frekvencijske karakteristike u frekvencijama koje se nalaze u vektoru f.

Pokušajte da iskoristite naredbu freqz bez izlaznih parametara, dakle samo freqz(b,a). Kakav rezultat se dobija?

Impulsni odziv filtra dobija se funkcijom impz(b,a,N), gdje su b i a brojnik i nazivnik funkcije prenosa filtra, respektivno, a Nje broj odmjeraka koji se ne mora zadati.

Simulacija digitalnog filtra može se izvršiti pomoću funkcije filter, čija je sintaksa:

Kao i do sada b i a su brojnik i nazivnik funkcije prenosa filtra, respektivno, a u vektorima x nalazi se ulazni signal. Vrijednosti odmjeraka izlaznog signala nalaze se u vektoru y.

Projektovanje IIR filtara

Tradicionalan pristup projektovanju IIR filtara sastoji se u projektovanju analognog filtra koji zadovoljava specifikacije i u njegovom preslikavanju u digitalni filtar. Ovaj pristup je dobar zato što su metode projektovanja analognih filtara su vrlo razvijene i jednostavne. Preslikavanje u digitalni domen vrši se pomoću sledećih metoda:

Obje funkcije kao argument primaju brojnik i nazivnik funkcije prenosa u analognom domenu, te frekvenciju odmjeravanja, a vraćaju brojnik i nazivnik funkcije prenosa u digitalnom domenu.

Zadaci

1. Korišćenjem metode impulsne invarijanse projektovati digitalni IIR filtar koji zadovoljava sledeće specifikacije:
   • jednolike oscilacije u propusnom opsegu 0 <= θ <= 0.2π rad,
   • maksimalno dozvoljeno slabljenje u propusnom opsegu 0.5dB,
   • nepropusni opseg  0.4π <= θ <= π rad,
   • minimalno slabljenje u nepropusnom opsegu 23dB,
   • period odmjeravanja π ms.
   1. Zahtjeve koje treba da zadovolji frekvencijska karakteristika filtra preslikati u analogni domen;
   2. Odrediti funkciju prenosa ekvivalentnog analognog filtra;
   3. Nacrtati amplitudnu i faznu karakteristiku analognog filtra;
   4. Preslikati funkciju prenosa analognog filtra u digitalni domen;
   5. Nacrtati amplitudnu i faznu karakteristiku digitalnog filtra;
   6. Uporediti dobijene frekvencijske karakteristike analognog i digitalnog filtra. Koje sličnosti možete uočiti? Koje razlike? Kakav uticaj ima promjena frekvencije odmjeravanja na frekvencijsku karakteristiku digitalnog filtra?
2. Ponoviti prethodni zadatak koristeći bilinearnu transformaciju.
3. Generisati 128 odmjeraka signala .
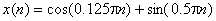   1. Nacrtati ovaj signal u vremenskom domenu i njegov spektar.
   2. Dovesti ovaj signal na ulaz filtara projektovanih u tačkama 1, odnosno, 2. Nacrtati izlazni signal. Dati komentar dobijenog rezultata.
   3. Nacrtati spektar signala na izlazu iz filtra. Da li rezultat odgovara vašim očekivanjima? Komentarisati!

Projektovanje FIR filtara

Najjednostavnija metoda za projektovanje FIR filtara je metoda prozorskih funkcija. Kod ove metode impulsni odziv FIR filtra dobija se kao:

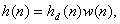
gdje je h_d(n) beskonačan impulsni odziv željenog (idealnog) filtra, a w(n) “prozor” konačnog trajanja. U MATLAB-u su implementirane sledeće prozorske funkcije:

Zadaci

1. Dat je idealni niskopropusni filtar:

   .

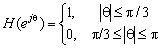   1. Nacrtajte frekvencijsku karakteristiku ovog sistema;
   2. Nacrtajte impulsni odziv ovog sistema;
   3. Da biste dobili FIR filtar na osnovu ovog IIR filtra, pomnožite impulsni odziv pravougaonom prozorskom funkcijom. Izaberite različite dužine prozorske funkcije, npr. 9, 21, 31, 51. Nacrtajte frekvencijske karakteristike dobijenih filtara. Posmatrajte širinu prelaznog opsega i slabljenje u nepropusnom opsegu. Šta se dešava sa povećanjem reda FIR filtra (dužine prozorske funkcije)?
   4. Pomnožite impulsni odziv IIR filtra Bartletovom, Hanningovom, Hammingovom i Blackmanovom prozorskom funkcijom dužine 31. Nacrtajte frekvencijske karakteristike dobijenih filtara. Posmatrajte širinu prelaznog opsega i slabljenje u nepropusnom opsegu. Šta se dešava sa povećanjem reda FIR filtra (dužine prozorske funkcije)?
   5. Na osnovu zapažanja iz prethodne dvije tačke pokušajte formulisati kako izbor vrste prozorske funkcije i njene dužine utiče na širinu prelaznog opsega i slabljenje u nepropusnom opsegu.